#apunte #matemáticas #mochila #destacado

Temario Prueba Matemática

Temas:

Lenguaje algebraico
Circunferencia y Círculo.

Los estudiantes deben ser capaces de:

Traducir expresiones del lenguaje natural al algebraico y viceversa
Reducir términos semejantes.
Valorizar expresiones algebraicas.
Identificar elementos básicos en una circunferencia.
Calcular el perímetro de una circunferencia, así como también el diámetro y el radio.
Calcular el área de un círculo.
Reconocer tipos de polígonos.
Aplicar la fórmula de suma de ángulos interiores en polígonos.
Aplicar la fórmula del ángulo interior en polígonos
Aplicar la fórmula de la suma de ángulos exteriores en un polígono.

1. Traducir expresiones del lenguaje natural al algebraico y viceversa

Significa convertir palabras en ecuaciones y ecuaciones en palabras.
Ej.: “el doble de x menos cinco” → $2 x - 5$ .
Solo debes identificar operaciones: sumar, restar, multiplicar, dividir.

2. Reducir términos semejantes

Consiste en juntar los términos que tienen la misma variable y exponente.
Ej.: $3 x + 5 x = 8 x$ . No se pueden unir términos distintos como $3 x$ y $4 y$ .

3. Valorizar expresiones algebraicas

Es reemplazar la variable por un número y calcular.
Ej.: Si $x = 2$ , entonces $3 x + 1 = 3 (2) + 1 = 7$ .

4. Identificar elementos básicos en una circunferencia

Debes reconocer: centro, radio, diámetro, cuerda, arco, circunferencia (el borde) y círculo (el interior).

5. Calcular el perímetro de una circunferencia, y su diámetro y radio

El perímetro se llama longitud y se calcula con:

$L = 2 π r$
o $L = π d$
Si tienes el radio puedes hallar el diámetro con $d = 2 r$ , y al revés $r = \frac{d}{2}$ .

6. Calcular el área de un círculo

Debes usar la fórmula:

A = π r^{2}

Es decir, π por el radio al cuadrado.

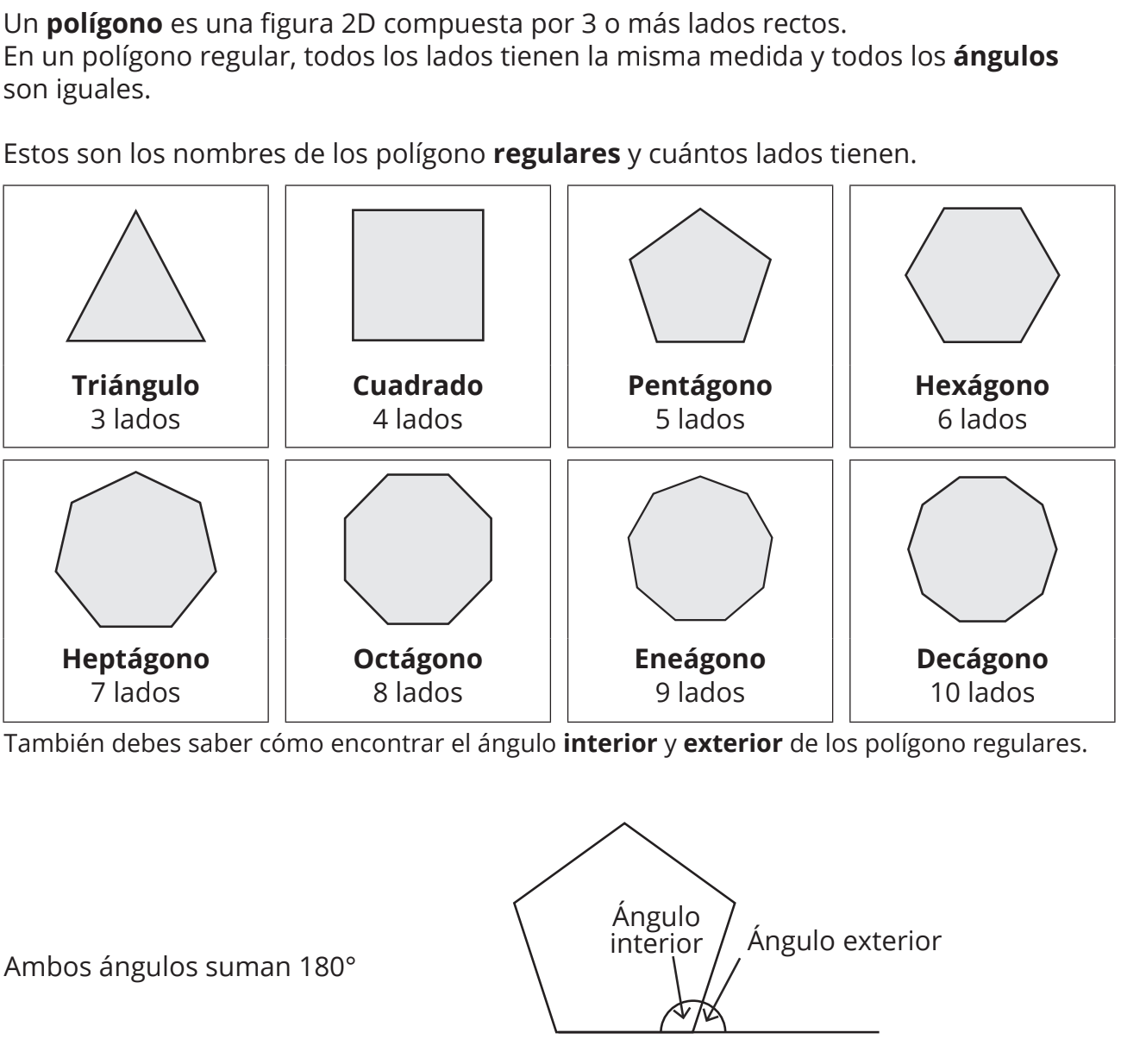
7. Reconocer tipos de polígonos

Debes identificar cuántos lados tienen y cómo se llaman:
Triángulo (3), cuadrilátero (4), pentágono (5), hexágono (6), etc.
Y distinguir si son regulares (todos iguales) o irregulares.

8. Aplicar la fórmula de suma de ángulos interiores en polígonos

Usa:

S = (n - 2) \cdot 180^{\circ}

donde n es el número de lados.
Solo reemplazas y calculas.

9. Aplicar la fórmula del ángulo interior en polígonos regulares

Si el polígono es regular (todos los ángulos iguales):

A_{int} = \frac{(n - 2) \cdot 180^{\circ}}{n}

10. Aplicar la fórmula de la suma de los ángulos exteriores en un polígono

Siempre vale:

S_{ext} = 360^{\circ}

En un polígono regular, cada ángulo exterior es:

A_{ext} = \frac{360^{\circ}}{n}

📐 Tabla de ángulos en polígonos regulares

Polígono	Suma de los ángulos interiores	Ángulo interior	Ángulo exterior
Ejemplo	(n – 2) × 180°	((n-2) × 180) / n	360 ÷ n
Triángulo (n=3)	(3–2)×180 = 180°	180 ÷ 3 = 60°	360 ÷ 3 = 120°
Cuadrado (n=4)	(4–2)×180 = 360°	360 ÷ 4 = 90°	360 ÷ 4 = 90°
Pentágono (n=5)	(5–2)×180 = 540°	540 ÷ 5 = 108°	360 ÷ 5 = 72°
Hexágono (n=6)	(6–2)×180 = 720°	720 ÷ 6 = 120°	360 ÷ 6 = 60°
Heptágono (n=7)	(7–2)×180 = 900°	900 ÷ 7 ≈ 128.57°	360 ÷ 7 ≈ 51.43°
Octágono (n=8)	(8–2)×180 = 1080°	1080 ÷ 8 = 135°	360 ÷ 8 = 45°
Eneágono (n=9)	(9–2)×180 = 1260°	1260 ÷ 9 = 140°	360 ÷ 9 ≈ 40°
Decágono (n=9)	(10–2)×180 = 1440°	1440 ÷10 = 144°	360 ÷ 10 = 36°

📹 *Videos: